《一級建築士学科試験》学科Ⅳ 構造【集中荷重が作用する交差梁の反力の比】

ブログやTwitterから建築士試験についてお伝えしています。

試験のポイントや考え方について自身の受験経験を基に記事を作成しています。
試験に向けての学習の補助として活用していただけると嬉しいです。

今回は、学科Ⅳ(構造)の過去問の中から、交差梁の反力の比について、試験的な考え方を解説します。（R2年度No.2）

著作権等の理由から、本記事では、試験問題を掲出しておりません。
以下のリンクより「過去の試験問題等(公益財団法人建築技術教育普及センター)」をご参照ください。

基本的な考え方

この問題の基本的な考え方は、長さが異なるA材・B材のたわみが等しいことから、それぞれにかかる集中荷重を求めていきます。

ここで使用する単純梁・集中荷重のたわみの公式は、以下の通りです。

この問題では、『A材とB材は、等質等断面』とあるため、A材とB材は、この式のうちのヤング係数[E]、断面二次モーメント[ I ]が同じになります。

また、題意より、交差梁の交差部のたわみ[ δ ]も等しいため、δ_A＝δ_Bが成立します。

そして、A材及びB材にかかる集中荷重をそれぞれ、P_A及びP_Bとして問題を解いていきます。

δ_A及びδ_Bは、それぞれ条件を当てはめると、以下のようになります。

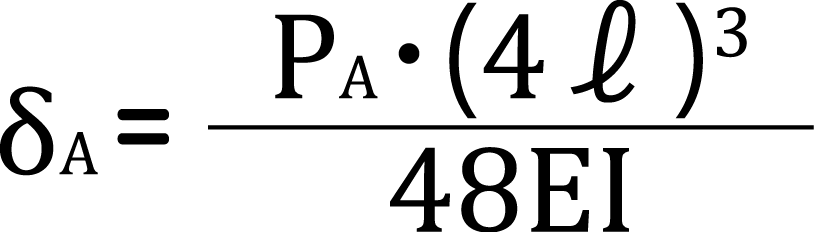
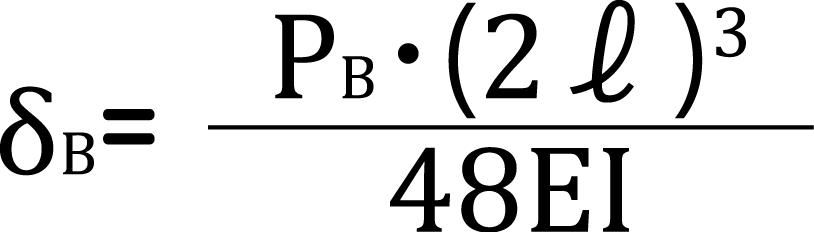
そして、δ_A＝δ_Bより、以下の等式が成立します。

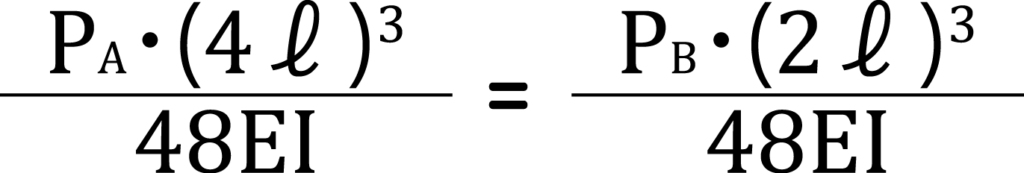
以上により、8P_A＝P_Bとなります。

そのため、A材・B材の反力R_A及びR_Bは、R_BがR_Aの8倍となることが分かります。

よって、［R_A：R_B＝1：8］になります。

ここまでの計算過程を見ると、A材・B材で異なるのは、梁の長さ(ℓ）のみで、単純梁・集中荷重のたわみの公式より、梁の長さの3乗の比になっている。

そして、A材・B材の長さの比は【2：1】のため、2³＝8より、［R_A：R_B＝1：8］であることが分かる。

たわみの計算問題は、たわみ量そのものを求める問題よりも、複数の部材のたわみ量の比や大小を求める問題が多いため、（公式を覚えていることを前提として）問題から計算に必要な数値の何が同じで、何が異なるのかに気づくことができれば、本問のように簡単な計算をするだけで正答することができます。