《一級建築士学科試験》学科Ⅳ 構造【断面寸法が異なる同材質のたわみ量の比】

建築技術研究所 です。

ブログやTwitterから建築士試験についてお伝えしています。

試験のポイントや考え方について自身の受験経験を基に記事を作成しています。
試験に向けての学習の補助として活用していただけると嬉しいです。

今回は、学科Ⅳ(構造)の過去問の中から、たわみ量の比較について、試験的な考え方を解説します。（R1年度No.2）

著作権等の理由から本記事では、試験問題を掲出しておりません。
以下のリンクより過去の試験問題等(公益財団法人建築技術教育普及センター)をご参照ください。

必要な公式

単純梁･集中荷重　たわみの公式

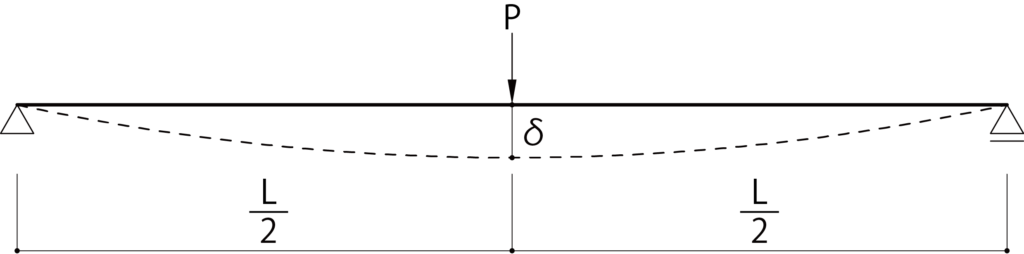
δ：たわみ，P：集中荷重，L：スパン長さ
E：ヤング係数，I：断面二次モーメント　

断面2次モーメントの公式

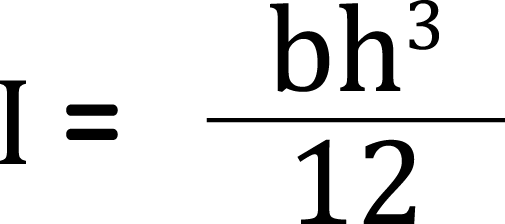
I：断面二次モーメント，ｂ：部材幅，ｈ：部材せい

基本的な考え方

本問では、『材料、スパンが同じ―』とあり、題意より【定数1/48】【集中荷重[P]】【ヤング係数[E]】【長さ[L]】が等しいため、断面2次モーメント[Ｉ]のみを比較すれば、解答できます。

そのため、下式の計算結果の比を求めます。

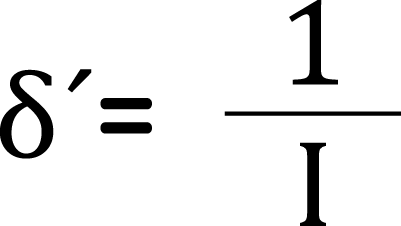
I_A＝2a*(2a)³/12＝16a⁴/12
→　δ_A＝12/16a⁴
I_B＝a*(2a)³/12*2＝8a⁴/12*2＝16a⁴/12
→　δ_B＝12/16a⁴
I_C＝2a*a³/12*2＝2a⁴/12*2＝4a⁴/12
→　δ_B＝12/4a⁴

以上により、たわみの比は以下のようになます。

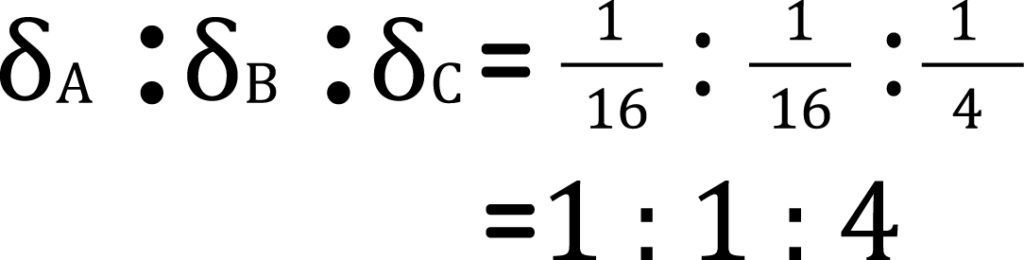
試験的な考え方

公式からわかるように、断面二次モーメントは部材幅より部材せいの大きさが影響しています。（せいの3乗に比例）

本問の場合、A,Bは部材せいが等しく、幅については、BはAの半分が2つ（＝等しい）ため、断面二次モーメントは、計算せずとも等しくなることが分かります。

また、Cは、せいがA及びBと比べて1/2で幅がA,B×2と等しいものが2つあります。
そのため、Cの断面二次モーメントはA及びBと比べて、(1/2)³×2＝1/4となることが分かります。

そのため、断面二次モーメントの逆数(1/I)となるたわみ量は、前項の通り、δ_A：δ_B：δ_C＝1：1：4となります。

このように、計算結果の比を答える問題の場合は、公式の成り立ちを理解すれば、選択肢を最大限に利用することにより、簡単な計算のみで正答肢を選ぶことができます。

まとめ