建築技術研究所 です。
ブログやTwitterから建築士試験についてお伝えしています。
試験のポイントや考え方について自身の受験経験を基に記事を作成しています。
試験に向けての学習の補助として活用していただけると嬉しいです。
今回は、前回の記事に引き続き、学科Ⅳ(構造)の過去問の中から、たわみ量の比較について、試験的な考え方を解説します。(R4年度No.2)
著作権等の理由から本記事では、試験問題を掲出しておりません。
以下のリンクより過去の試験問題等(公益財団法人建築技術教育普及センター)をご参照ください。
- 計算しない
- 選択肢を有効活用する
計算しない
R4年No.2は、前回の記事でお伝えしたR1年No.2の類似問題になります。
R4年の問題では、R1年の問題と異なり、たわみ量の大小だけを比較すればよいため、具体的な計算が必要なく、イメージさえできれば正答できます。
『Don’t think. Feel!』です。
問題の基本的な進め方は、R1年の問題と同じく、断面二次モーメント[I]を比較すればよいです。
(以下の公式のうち、集中荷重[P]、長さ[L]、ヤング係数[E]は等しく、たわみ量の比較に影響しないため、考慮しません。)

ここで注目するのは、【断面寸法】と【選択肢】です。
断面二次モーメントは、下式の通り、部材せいの3乗に比例し、部材幅よりも部材せいが影響することから、梁Cは、梁A及び梁Bと比べて部材せいが大きいため、断面二次モーメントが最も大きいことが分かります。
つまり、断面二次モーメントの逆数となるたわみ[ δC ]は、最も小さくなります。(前回記事『基本的な考え方』参照)
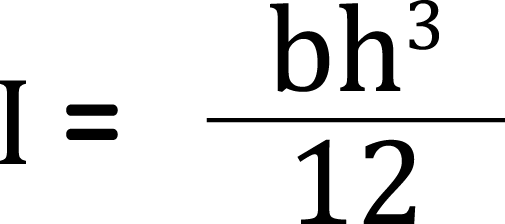
選択肢を有効活用
ここで、選択肢1.~4.を確認します。選択肢は、以下のようになっています。
- δA<δB=δC
- δA=δB<δC
- δB=δC<δA
- δC<δA=δB
選択肢を確認するときに注目するのは、前項の通り、[ δC ]が最も小さくなっているかです。
選択肢1.及び2.は、δCが、δAもしくはδBのたわみよりも大きくなっているため、不適当です。
次に、選択肢3.は、δCが、δAよりも小さくなっていますが、δBと等しいことになっています。
梁Bは、梁Cの部材の半分のものが2つ重なっている(幅は2倍)ため、断面二次モーメントが3乗に比例することを知っていれば、等しくなることはないとイメージできると思います。
(実際に計算すると、IB=a4/2、IC=2a4)
そのため、選択肢3.は不適当です。
選択肢4.は、δCが、δA及びδBのたわみよりも小さくなっており、そのような選択肢がひとつしかないため、正答肢であることがわかります。
なお、計算するとδA=δBとなるのですが、適当な選択肢が4.しかないため、検討する必要はありません。
まとめ
- 計算しない
- 選択肢を有効活用する


